Extend previous understanding of multiplication and division to compute products and quotients of positive fractions by positive fractions, including mixed numbers, with procedural fluency.

Solve multi-step real-world problems involving any of the four operations with positive multi-digit decimals or positive fractions, including mixed numbers.

Rewrite positive rational numbers in different but equivalent forms including fractions, terminating decimals and percentages.

Using the following algorithms will help students perform fraction multiplication and divison quickly. However, these algorithms do not help students understand the concept of fraction multiplication and division, nor do they help students decide when to multiply vs. divide in a given real-world situation. Therefore, students need careful practice to understand the difference. Some students will understand this concept quickly; some will take more time. Please read on to see tips for helping students gain this conceptual understanding through work with visual models.

Fraction multiplication is related to the idea of “scaling.” It can be conceptually difficult for students who are used to the idea that multiplication always results in a larger number.

Helping students conceptualize fraction multiplication with models, as shown below, is useful until they understand how to use the algorithm appropriately.

“I had half of a cake. Then, I ate half of it. What fraction of the original cake do I have left?”

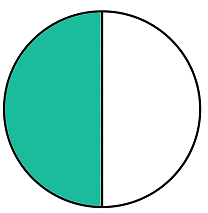
Let's start by looking at the half of the cake. If we are eating half of a half, we are ending up with a smaller portion of cake than we started with.

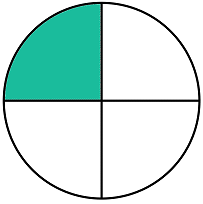
Cutting the half of cake leftover into halves (and generalizing that cut to the rest of the cake) shows that the resulting piece, the half of a half, is equal to one-fourth.

“What is one-third of one-fourth?”

Let's start with a fraction diagram that models 1/4.

Then, we will model 1/3 of 1/4 by dividing our 1/4 into thirds. We will extend the lines. This way, we can see our new denominator.

Dividing the 1/4 into thirds actually created twelfths. 1/3 of 1/4 is 1/12.

When discussing division with whole numbers, we think of the idea "groups of," as in "How many groups of 6 can I make from 36?" This idea is integral to understanding the concept of fraction division. Just like with fraction multiplication, students can have some conceptual misunderstandings if they are used to the idea that division always results in a smaller number.

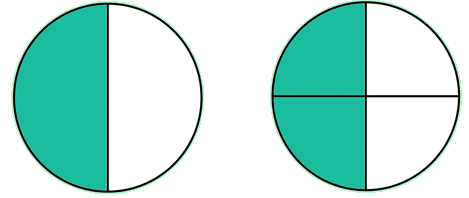
This problem means "How many groups of 1/4 can I make out of 1/2?" or "How many one-fourths are there in one-half?"

Let's consider this real-world situation: “I had half of a cake. I want to find how many one-fourth cake servings there are in this portion of cake.”

The model shows that there are 2 one-fourth servings in the 1/2 cake. The answer to the division problem is 2.

If I have 5/8 of a cake, how many 1/4 servings do I have?

In this example, it's helpful to think of the relationship between eighths and fourths. Every 2 eighths is equal to 1 fourth, so we can visualize this situation like this:

Now, we can count the number of fourths created. We made 2 fourths, plus half of another fourth.

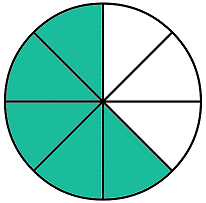
Using the algorithm, as shown below, leads to the same answer.